在数学运算中,分数乘法计算是极为重要的一部分,掌握分数乘法的计算方法和规则,不仅有助于解决日常生活中的实际问题,也是学习数学的基础,本文将详细介绍分数乘法的概念、计算方法以及实际应用。
分数的概念
分数是一种数学表达方式,用于表示整体的一部分,分数由两个部分组成:分子和分母,分子表示部分的数量,而分母则表示整体的数量,1/2表示整体的一半。
分数乘法的基本原理
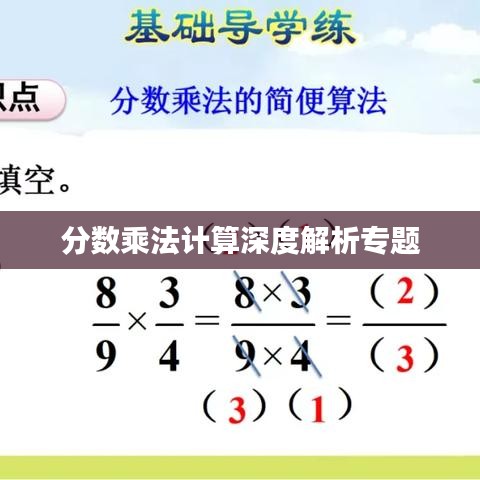
分数乘法计算基于这样一个原理:分数的分子乘以分子,分母乘以分母,如果有两个分数a/b和c/d,它们的乘积是(a × c) / (b × d)。
分数乘法计算步骤
1、确定两个分数的分子和分母。
2、按照分数乘法的原理,将分子相乘得到新的分子,将分母相乘得到新的分母。
3、简化得到的分数,即将其化为最简形式。
分数乘法计算的特殊情况
1、分数乘以整数:当其中一个分数乘以一个整数时,只需将整数看作分母为1的分数,然后按照普通分数乘法的规则进行计算。
2、分数乘以小数:将小数转化为分数,然后按照普通分数乘法的规则进行计算。
实际应用
分数乘法在实际生活中有广泛的应用,例如在计算面积、处理比例问题、计算速度等方面,掌握分数乘法计算技巧,可以更加准确地解决这些问题。
实例解析
假设我们要计算两个分数的乘积:3/4和5/8,我们将分子相乘得到新的分子:3 × 5 = 15,我们将分母相乘得到新的分母:4 × 8 = 32,3/4乘以5/8等于15/32,我们将这个分数化为最简形式,得到答案为3/8,这就是分数乘法的计算过程。
练习与提高
为了熟练掌握分数乘法计算技巧,需要进行大量的练习,可以通过课本、习题集、在线资源等途径获取练习题,通过不断的练习,提高计算速度和准确性,也可以尝试解决一些实际问题,如计算面积、处理比例问题等,以检验自己的掌握程度。
分数乘法计算是数学运算中的重要部分,掌握其原理和技巧对于解决实际问题以及深入学习数学具有重要意义,本文详细介绍了分数乘法的概念、计算方法、特殊情况以及实际应用,并通过实例解析和练习与提高部分帮助读者更好地理解和掌握分数乘法计算技巧,希望读者能够认真学习和实践,不断提高自己的数学能力。
转载请注明来自西北安平膜结构有限公司,本文标题:《分数乘法计算深度解析专题》








 鲁ICP备16008434号-2
鲁ICP备16008434号-2
还没有评论,来说两句吧...